I. AVANT- PROPOS
a.
b.Définitions
II. LES CARTES
a. Echelle d’une carte
b.Les projections
c. Les projections par développement
III. LES TROIS NORDS
a. Définitions/figuratif
b.Relations
angulaires entre les trois Nords
IV.
LES DIRECTIONS
I. AVANT- PROPOS
a.
Troisième planète du système solaire
dans l’ordre croissant des distances au Soleil, la terre a la forme d’une
sphère légèrement aplatie aux pôles, dont le rayon moyen est de
Le géoïde est le volume défini par la surface courbe du niveau moyen des mers supposé prolongé sous les continents. Il correspond conventionnellement à l’altitude 0.
Une ellipsoïde de révolution est le volume engendré par une ellipse tournant sur l’un de ses axes. La sphère terrestre est définie selon différents types d’ellipsoïdes servant de référence pour l’établissement des cartes.
ELLIPSOÏDE INTERNATIONALE DE HAYFORD (1924 – CARTES UTM)
- demi-grand axe :
- demi-petit axe :
- rayon moyen :
- aplatissement : 1/297
ELLIPSOÏDE DE CLARKE (1880 – CARTES LAMBERT)
- demi-grand axe :
- demi-petit axe :
- rayon moyen :
- aplatissement : 1/293
Autres : ELLIPSOÏDE DE EVERESTE ET DE BESSEL
L’aplatissement est le rapport de la différence des 2 axes de l’ellipse sur le grand axe.
b.Définitions
Pôle :
chacune des deux extrémités de l’axe de rotation de
Verticale :
Direction suivant laquelle s’exerce la pesanteur. Elle est donnée par la
direction que prend le fil à plomb en un point A quelconque de la surface de
Plan Horizontal : En un point A quelconque, c’est le plan perpendiculaire à la verticale.
Méridien :
- ligne imaginaire joignant un pôle à l’autre par la surface terrestre.
- demi-grand cercle passant par les pôles
- ligne imaginaire formée par une juxtaposition de points situés à la même longitude
Parallèle :
- chacun des cercles imaginaires parallèles à l’équateur
- cercle imaginaire formé par une juxtaposition de points situés à la même latitude. Les tropiques du Cancer (hémisphère Nord) et du Capricorne (hémisphère Sud) sont de parallèles remarquables du globe terrestre.
Equateur :
- grand cercle du globe dont le plan est perpendiculaire à l’axe des pôles.
- C’est le parallèle équidistant des deux pôles.
Latitude : c’est l’angle que fait la verticale d’un lieu avec le plan équatorial. L’Equateur est à la latitude 0°, les pôles sont à la latitude 90°. La latitude est dite Nord (N) de l’Equateur vers le pôle Nord, et inversement.
Colatitude : c’est l’angle complémentaire de la latitude. C’est donc l’angle que fait la verticale d’un point avec le plan polaire.
Longitude : c’est l’angle déterminé entre le plan méridien du lieu avec le plan du méridien origine passant par Greenwich, près de Londres. La longitude se mesure en degrés de 0 à 180° par rapport au méridien origine, soit vers l’Est (E), soit vers l’Ouest (W).
Mille marin : c’est la longueur de l’arc d’une minute sexagésimale de latitude prise sur un méridien. Par la déformation de la sphère terrestre, cette longueur n’est pas identique au pôle et à l’équateur :
- Pôle :
- Equateur : 1852,
Par convention, la
valeur retenue pour le mille marin est de
Grand cercle : c’est la plus grande circonférence
de la sphère terrestre dont le lan passe par le
centre de
Arc de grand cercle : portion de grand cercle qui sera représenté sur toute carte par une courbe (exception : carte gnomonique). Deux points de positions quelconques sur le globe sont toujours sur un arc de grand cercle quelconque. Ils sont reliés, d’une part, par l’arc mineur et d’autre part, par l’arc majeur.
Orthodromie :
- route la plus courte entre deux points, suivant le tracé d’un arc de grand cercle
- trajet suivi par les ondes électromagnétiques.
Loxodromie :
- courbe de la sphère terrestre qui coupe les méridiens sous un angle constant
- c’est la route suivie par un mobile qui se dirige au compas (boussole).
- la loxodromie qui correspond à la route suivie par un mobile gardant un cap constant est représentée par une droite les cartes en projection conforme (Lambert).
II. LES CARTES
Définition : c’est la représentation sur un plan des mouvements du sol (nivellement) et des détails superficiels d’une portion de la surface terrestre (planimétrie).
a. Echelle d’une carte
Le problème consiste à représenter une surface relativement grande de terrain sur un plan de surface réduite. Cette représentation est faite suivant un rapport de réduction appelé échelle.
L’échelle est le rapport linéaire constant qui existe entre la longueur « l » d’une ligne mesurée sur la carte et la longueur « L » de la ligne correspondante mesuré » sur le terrain suivant l’horizontale.
Sur une carte, on distingue l’échelle numérique de l’échelle graphique.
- L’échelle numérique :
o c’est une fraction de la forme 1/ N, où plus « N » est petit, plus l’échelle est grande.
o Les cartes sont classées en trois catégories
§ Les cartes à grande échelle : plan directeur au 1/10 000, au 1/20 000, et cartes au 1/25 000
§ Les cartes à moyenne échelle : carte au 1/50 000 et au 1/100 000
§ Les cartes à petite échelle : carte au 1/200 000 couleur, au 1/200 000 MICHELIN, au 1/250 000, au 1/500 000 et au 1/1 000 000
o Pour utiliser l’échelle numérique, il faut s’astreindre à lire la
fraction en réalisant que «
- L’échelle graphique :
o C’est un dessin, figuré en général au bas de la carte, qui matérialise l’échelle numérique. Elle est constituée par une ligne divisée en segments, représentant l’unité de mesure réduite à l’échelle de la carte.
o Le segment de gauche, appelé TALON, est divisé en sous-multiples de l’unité de mesure. Pour la carte au 1/50 000, l’échelle est divisée en kilomètres, le talon est divisé en hectomètres.
o Cette échelle graphique est utilisée lorsqu’on ne dispose pas de règle millimétrée, pour mesurer la distance topographique entre deux points, directement sur la carte, par exemple à l’aide d’une cordelette.
b.Les projections
1. Choix de l’ellipsoïde
Différents ellipsoïdes ont été déterminés pour matérialiser le globe terrestre. Parmi les plus connus et utilisés, ceux de CLARK et de HAYFORD.
Pour l ‘établissement des cartes militaires françaises, ont été adopté l’ellipsoïde de CLARKE (1880) dans la projection LAMBERT, et l’ellipsoïde de HAYFORD (1910) dans la projection UTM.
2. Transformation de l ‘ellipsoïde en plan
A chaque point P du terrain on fait correspondre un point p, défini par la verticale du point P sur l’ellipsoïde de référence.
La surface de l’ellipsoïde ne pouvant être étendue sur un plan sans déchirures ni déformations, il est donc impossible d’en donner une représentation plane rigoureuse. Pour réduire ces déformations on a recours à des lois de correspondance mathématiques entre les points de l’ellipsoïde et leur représentation sur le plan. Ces lois définissent des systèmes de projection.
On distingue trois systèmes principaux de projection :
- Les projections perspectives :
o Principe : chaque point est projeté sur un plan de projection
o Inconvénient : grandes déformations lorsqu’on s’éloigne du point de contact.
- Les projections polyédriques :
o Principe : globe à facettes
o Inconvénient : problème de « raccords » entre chaque facette et sa voisine
o Avantage : projections équivalentes, elles conservent les surfaces.
- Les projections par développement
o Principe : projection sur une surface développable, tangente ou sécante le long d’un parallèle ou d’un méridien.
§ Surfaces cylindriques : projection de MERCATOR, projection UTM
§ Surfaces coniques : projection, de BONNE, projection de LAMBERT
Il est à noter que : - tous les systèmes déforment les longueurs
-
certains conservent les surfaces et sont dits équivalents
-
certains conservent les angles et sont dit conformes
AUCUN
SYSTEME NE PEUT ÊTRE A
Entre tous les systèmes de projection, le choix s’exerce d’après la destination prévue pour la carte. Ainsi :
- la navigation exige une rigoureuse précision des directions. On utilisera pour cet usage une carte en projection conforme qui respectera les valeurs angulaires® LAMBERT ou UTM
- le cadastre exige un rapport exact des surfaces. On utilisera des acrtes ouplans établis dans une projection équivalente respectant le rapport des surfaces® BONNE
- l’armée française, après avoir préféré l’exactitude des distances, recherche depuis 1914 la précision des directions nécessaire dans la préparation des tirs à longue portée, précision qui devient de plus en plus impérative avec l’apparition des fusées intercontinentales. (donc projection conforme !)
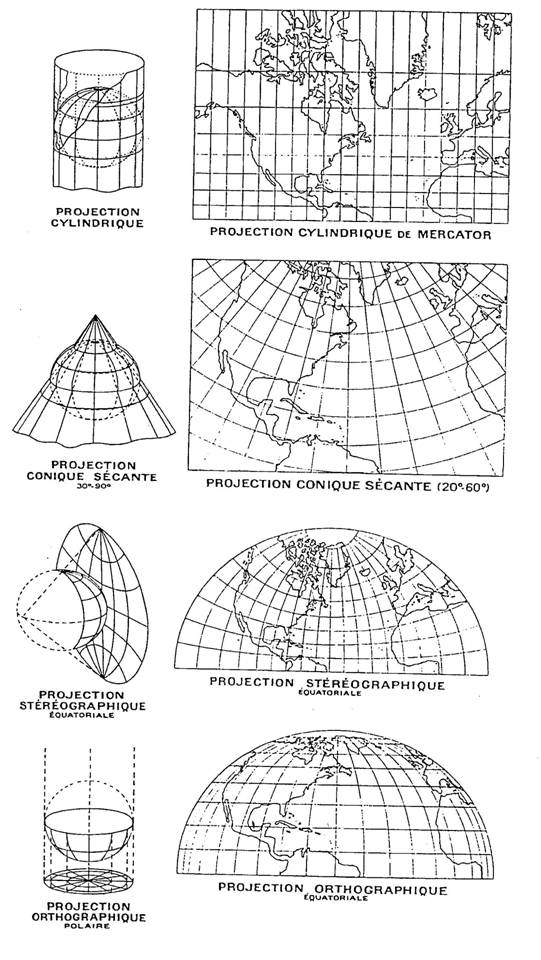
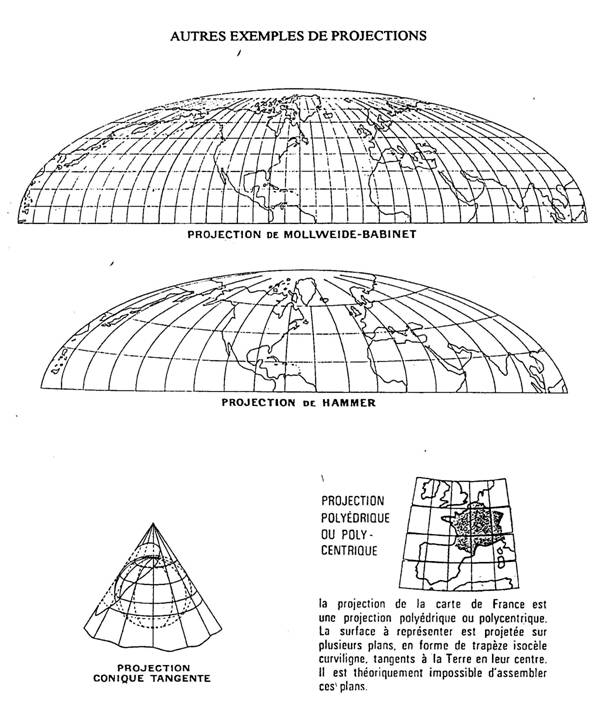
3. Les projections par développement
Projection
conique de base
Le canevas est projeté sur un cône tangent ou sécant, en contact avec la sphère sur un parallèle. Fendu le long d’un méridien et déroulé, ce cône donne un plan sur lequel les méridiens sont représentés par un éventail de droites concourantes au pôle.
Les parallèles sont des arcs de cercles concentriques au pôle.
Les déformations sont faibles le long du parallèle de contact mais augmentent lorsqu’on s’en éloigne.
Cette projection n’est ni conforme ni équivalente.
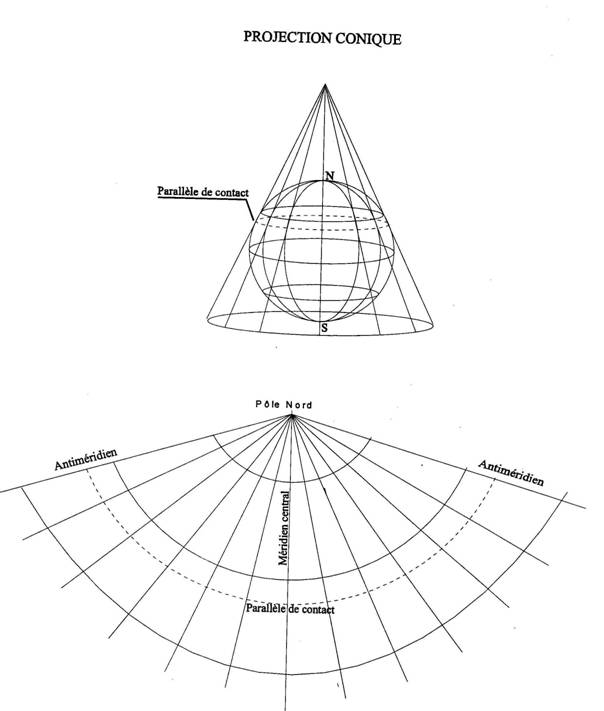
Projection
conique conforme de LAMBERT
Pour conserver les valeurs angulaires et rendre la carte conforme on est conduit à modifier l’écartement des parallèles sur la représentation plane.
Les distances ne sont conservées que sur les deux parallèles moyens équidistants du parallèle de contact, centré sur la zone à représenter.
Les méridiens sont des droites concourantes au sommet du cône de projection et présentent entre eux des angles proportionnels aux différences de longitude.
Les arcs de grands cercles sont des courbes,
mais dans la zone centrale de la projection (à proximité du parallèle de
contact), on peut avec une bonne approximation les confondre avec une droite
sur une distance de
Pour
que les altérations apportées par ce type de projection ne deviennent pas trop
importantes, on en réduit l’application à une zone limitée. Il en résulte que
son application à un pays comme
Projection
équivalente de BONNE
Dérivée comme celle de LAMBERT de la projection conique simple, les parallèles n’ont pas été modifiés mais les méridiens, à l’exception du méridien central, sont déformés de façon à rendre la représentation équivalent.
Le canevas représente les parallèles par d’autres courbes concentriques aux pôles.
Ce mode de projection a été utilisé pour l’établissement des au 1/80 000 dites d’Etat-Major, remplacées aujourd’hui par les nouvelles cartes en projection LAMBERT au 1/50 000.
Projection
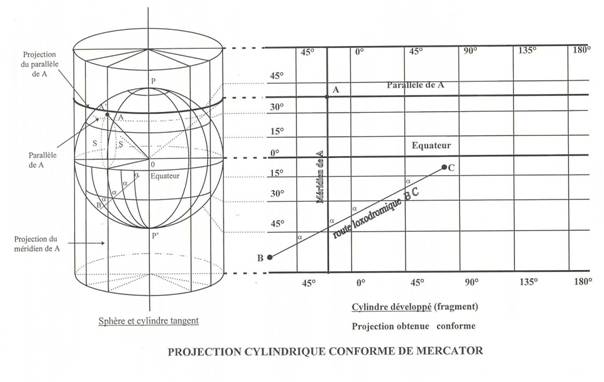
cylindrique de MERCATOR
On considère un cylindre tangent à la sphère terrestre le long de l’équateur.
En développant le cylindre les méridiens se trouvent représentés par des droites parallèles perpendiculaires à l’équateur, lui-même représenté par une droite. On obtient ainsi un réseau orthogonal de méridiens et de parallèles.
Les parallèles, tout comme dans la projection de LAMBERT, ont un écartement croissant en se rapprochant des pôles, afin de rendre la projection conforme.
Dans la zone de 200 à
Les arcs de grands cercles sont représentés
par des courbes que l’on peut assimiler à des droites jusqu’à
La projection étant rendue conforme, la route loxodromique (à cap constant coupant les méridiens selon un angle constant) est représentée par une droite. Lorsque deux points sont à la même longitude (sur un méridien) ou sur l’équateur, loxodromie et orthodromie se confondent.
Cette projection, malgré ses inconvénients, est utilisée jusqu’aux latitudes de 60° pour l’établissement des planisphères, et pour les cartes marines qui permettent la navigation à cap constant, donc le tracé de la courbe loxodromique par une droite.
Projection
de GAUSS et projection UTM
Seul le découpage de
Le système MERCATOR est une projection
correspondant au développement d’un cylindre circonscrit à
C’est l’appellation anglaise UNIVERSAL TRANSVERSE MERCATOR qui a prévalu et le système international a pris le nom de projection Universelle Transverse de Mercator : U.T.M..
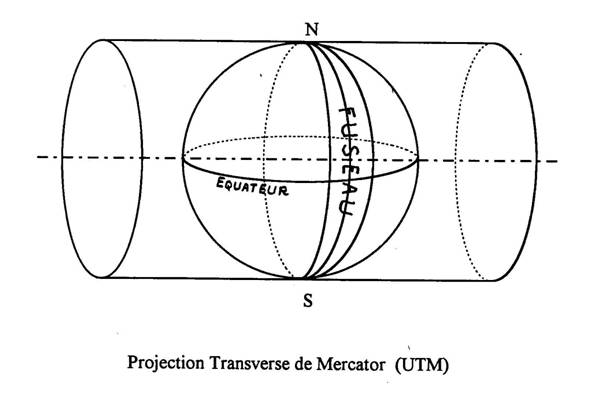
III. LES TROIS NORDS
a. Définitions/figuratif
Le Nord Géographique, (NG ou ) :
C’est la direction indiquée par l’étoile polaire.
C’est le point de convergence de tous les méridiens de l’hémisphère Nord (ou hémisphère boréal).
C’est la direction indiquée par le
méridien du lieu où l’on se trouve.
Le Nord Magnétique (NM ou )
C’est la direction indiquée par l’aiguille magnétique de la boussole.
Elle forme avec la direction du Nord Géographique un angle appelé DECLINAISON, variable en fonction du lieu et du temps.
Le NORD DE
Il est donné par une droite parallèle à l’axe des « Y » du quadrillage de la carte.
- NL pour le Nord LAMBERT (cartes LAMBERT)
- GN pour GRID NORTH (cartes UTM)
- Quel que soit le type de projection, on utilise également le « Y » puisque parallèle à l’axe des Y du carroyage.
FIGURATIF :
La disposition de ces trois Nords les uns par rapport aux autres est matérialisée par
un schéma donnant la valeur des angles, dessiné en marge des cartes et que l’on
nomme FIGURATIF.
FIGURATIF
b.Relations
angulaires entre les trois Nords
1. La déclinaison magnétique (D)
C’est l’angle formé en un point par la direction du Nord magnétique (NM) avec la direction du Nord Géographique (NG).
Actuellement, en France, D est occidentale : elle fait un angle vers l’ouest.
La déclinaison magnétique n’est pas constante,
- variation en fonction du temps :
o séculaire : la déclinaison varie lentement au cours des années. Elle est actuellement occidentale et varie d’environ 6 minutes par an. Le pôle magnétique se trouve aux environs de la base américaine de THULE.
o Diurne : la variation est périodique dans la journée, et chaque jour la déclinaison reprend une même valeur aux environs de 10H00 et de 18H00. C’est par cette valeur qu’est définie la déclinaison d’un point. Une variation saisonnière est également opbservée, maximale en juin et minimale en septembre.
- variations en fonction du lieu : les valeurs de la déclinaison sont obtenues expérimentalement en mesurant en de nombreuses stations l’azimut d’un barreau aimanté suspendu horizontalement.
2. La déclinaison magnétique rapportée (d)
C’est l’angle fait en un point par la direction du Nord magnétique avec la direction du Nord de la carte.
Du fait de la variation du Nord Magnétique décrite supra, cet angle subit les mêmes variations que D.
3. La convergence des méridiens
C’est l’angle fait en un point par la direction du Nord de la carte (axe des « Y ») par rapport à la direction du Nord Géographique.
La valeur de cet angle est fonction de la position relative des deux Nords au point considéré, elle-même déterminée par la situation géographique de ce point.
Il peut être en effet situé sur le méridien origine, à l’Est ou encore à l’Ouest (méridien de PARIS pour les cartes LAMBERT ou méridien central du fuseau pour les cartes UTM).
IV. LES DIRECTIONS
a. Définitions
- DIRECTION : une direction quelconque A-B est définie par l’angle qu’elle forme avec une direction origine ou direction de référence issue du point A.
Le
sens de l’angle est toujours compté à partir de la direction origine et dans le
sens des aiguilles d’une montre.
Les directions de référence sont :
o le Nord Géographique (NG)
o le Nord de la carte (Y)
o le Nord Magnétique (NM)
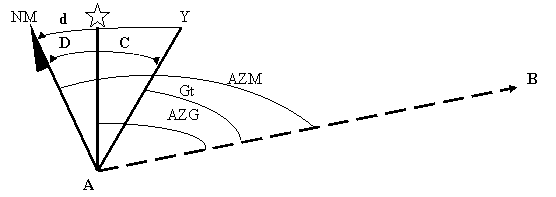
Avec une direction A-B quelconque, les trois Nords déterminent trois angles :
- L’azimut géographique (AZG)
C’est l’angle formé par la direction A-B et le Nord Géographique.
- Le gisement (Gt)
C’est l’angle formé entre la direction A-B et le Nord de la carte.
- l’azimut magnétique
C’est l’angle formé entre la direction A-B et le Nord Magnétique
b.Relations entre Gt
– AZM – AZG
Suivant la position relative du Nord de la carte par rapport au Nord Géographique, on aura les relations suivantes :
- A est situé à l’Ouest du méridien origine LAMBERT ou du méridien central UTM :
Gt = AZM – d
B
AZM = Gt + d
AZG = AZM – D
Gt = AZG + C
- A est situé à l’Est :
Gt = AZM – d
AZM = Gt + d
AZG = AZM – D
Gt = AZG – C
-
Y
A est situé sur le méridien origine LAMBERT ou sur le méridien
central du fuseau UTM:
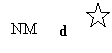
Gt = AZM – d
AZM
D
= AZM – D
AZG B
AZM = Gt + d
= Gt = D
Gt
AZG = AZM – d
= AZM – D
A
Gt = AZG